Una red neuronal artificial (RNA) es un modelo matemático inspirado en cómo funciona el cerebro humano. En lugar de utilizar neuronas biológicas, utiliza neuronas artificiales, que son funciones matemáticas capaces de recibir datos, procesarlos y transmitir un resultado.
Este sistema permite que la red aprenda, a partir de datos, y tome decisiones o haga predicciones.Cada neurona artificial realiza un cálculo sencillo: recibe varias entradas (por ejemplo, los valores de píxeles de una imagen), les aplica unos pesos que indican su importancia, suma esos valores y luego aplica una función de activación, que decide si la neurona “se activa” o no. Este resultado se transmite a la siguiente capa de la red.
La fórmula básica que usa cada neurona es algo así como:
salida = f(w₁x₁ + w₂x₂ + … + wₙxₙ + b)
donde f es la función de activación, los w son los pesos y b es un valor adicional llamado «bias» o sesgo.
Como están formadas las redes neuronales
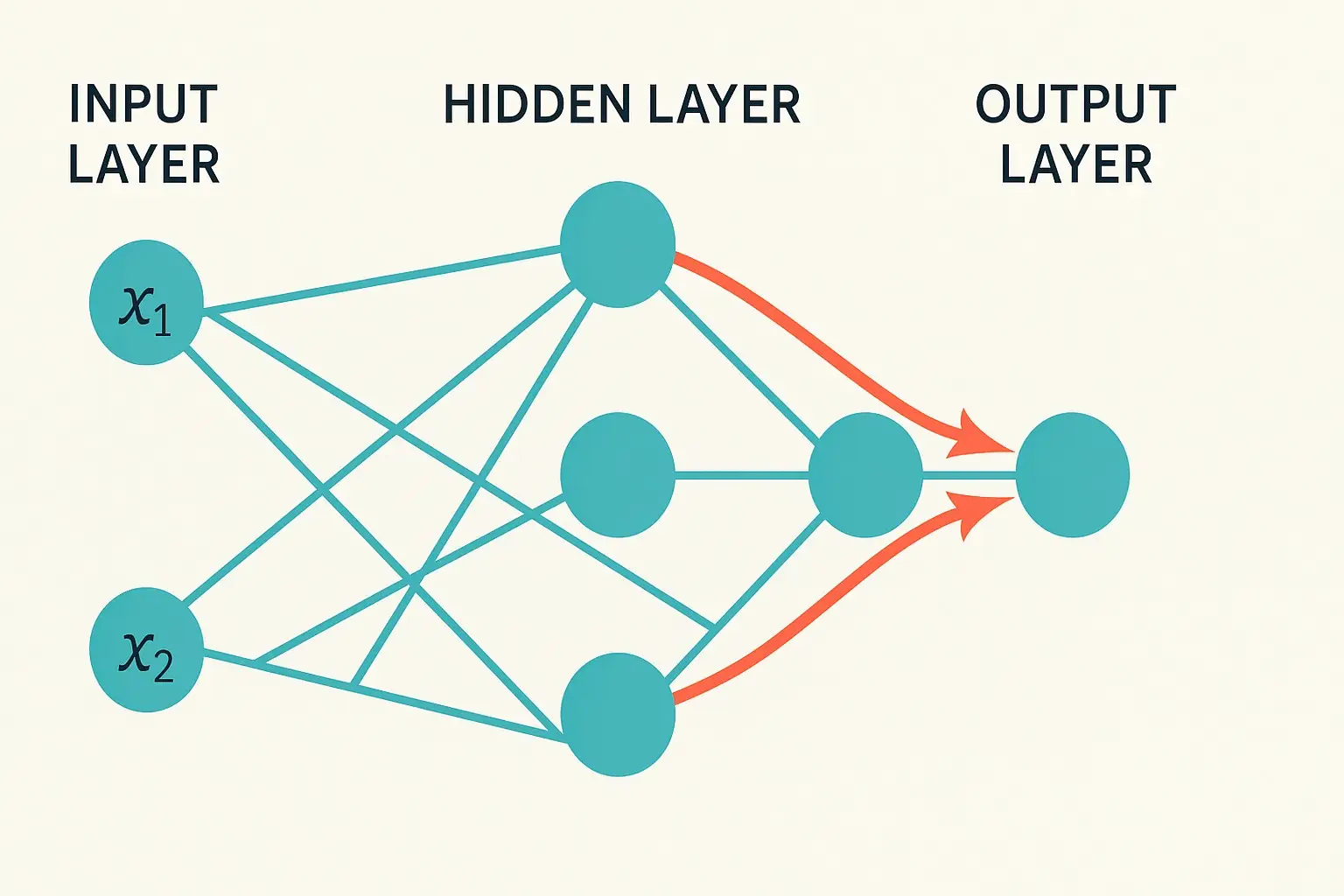
Las redes neuronales están formadas por capas de neuronas. La capa de entrada recibe los datos (como los píxeles de una imagen o palabras de una frase), las capas ocultas procesan esos datos internamente, y finalmente, la capa de salida genera la respuesta, como una clasificación o una predicción. Cuantas más capas ocultas tiene una red, más compleja y profunda se vuelve (por eso se llama deep learning cuando se usan muchas capas).
El proceso de aprendizaje de una red neuronal ocurre durante la fase de entrenamiento. Primero, se le presentan muchos ejemplos con sus respectivas respuestas correctas (por ejemplo, imágenes de dígitos y su valor). La red intenta hacer una predicción, y luego se compara esa predicción con la respuesta real. El error que comete se calcula usando una función de pérdida. A partir de ese error, se usa un proceso llamado retropropagación para ajustar los pesos de cada conexión entre neuronas, de manera que la red aprenda a mejorar su rendimiento. Para hacer estos ajustes se utiliza un algoritmo llamado descenso de gradiente, que va modificando los valores de los pesos poco a poco para minimizar el error.
Red Neuronal Entrenada (RNE)
Una red neuronal entrenada para reconocer dígitos escritos a mano puede recibir imágenes en blanco y negro de 28×28 píxeles, lo que representa 784 datos de entrada. Esos datos atraviesan varias capas, y la capa final tiene 10 neuronas, una para cada dígito del 0 al 9. La neurona con el valor más alto será la que indique cuál número cree la red que hay en la imagen.
Tipos de Redes Neuronales
- Las redes totalmente conectadas (o perceptrones multicapa) son las más básicas y se usan para tareas generales.
- Las redes convolucionales (CNN) están diseñadas para procesar imágenes, porque pueden detectar patrones visuales como bordes, texturas o formas.
- Las redes recurrentes (RNN), por otro lado, tienen “memoria” y se utilizan para trabajar con datos secuenciales, como texto, audio o series temporales.
- Los transformers, que son una evolución más reciente, han revolucionado el procesamiento de lenguaje natural y son la base de modelos como ChatGPT.
Estas redes funcionan tan bien porque pueden aprender representaciones internas complejas de los datos, sin necesidad de que los humanos les digan explícitamente qué buscar. Si están bien entrenadas, pueden generalizar a datos que no han visto antes y resolver tareas que serían extremadamente difíciles de programar de forma tradicional.
Paso a Paso de una Red Neuronal Simple
📍 Paso 1: Entrada de Datos (Input Layer)
Supongamos que tenemos 2 entradas:
- x1 =0.6
- x2 =0.4
📍 Paso 2: Asignación de Pesos y Bias
Cada entrada se conecta a una neurona de la capa oculta, cada conexión tiene un peso (w) y la neurona tiene un bias (b).
Por ejemplo, para una sola neurona en la capa oculta:
- Peso w1 = 0.5 para x1
- Peso w2 = -0.7 para x2
- Bias b = 0.1
📍 Paso 3: Cálculo del valor ponderado
Se calcula la suma ponderada:
- z = (x1 × w1) + (x2 × w2) + b
- z = (0.6 × 0.5) + (0.4 × −0.7) + 0.1 = 0.3 − 0.28 + 0.1 = 0.12
📍 Paso 4: Aplicación de función de activación
Se aplica una función de activación para introducir no linealidad.
Por ejemplo, usando la función sigmoide:
- σ(0.12) ≈ 0.53
Esto es la salida de la neurona oculta.
📍 Paso 5: Cálculo en la capa de salida
Supongamos que esta neurona se conecta a una sola neurona de salida:
- Peso hacia la salida: Wo = 0.8
- Bias de salida: Bo = −0.2
Zo = (0.53 × 0.8) + (−0.2) = 0.424 − 0.2 = 0.224
Aplicamos de nuevo la función de activación: σ(0.224) ≈ 0.56
Este es el resultado de la red neuronal simple.
📍 Paso 6: Cálculo del error y retropropagación (Backpropagation)
Se compara la salida obtenida (0.56) con la salida esperada (y), por ejemplo, y=1
Se calcula el error (por ejemplo, usando error cuadrático): E= ½ (y−y^) 2 = ½ (1−0.56) 2 ≈ 0.097
Con este error, la red ajustará los pesos y biases utilizando gradiente descendente y retropropagación.
🎯 Resumen conceptual
- Entrada → Suma ponderada → Activación → Salida.
- Se calcula error → Se ajustan pesos y biases.
- Repetir proceso hasta que el error sea mínimo.